Termodinámica 1.1
7.3.1. Cambio de disponibilidad de energía (energía) de un sistema.
7.4. Transferencia de energía por calor, trabajo y masa.
La exergía al igual que la energía, puede transferirse hacia o desde un sistema en tres formas: calor, trabajo y flujo másico.
Transferencia de exergía por Calor, Q
Esta relación da la trasferencia de exergía que acompaña la transferencia de calor de Q siempre que T sea mayor o menor que To.
Observe que la transferencia de calor debida a una diferencia finita de temperatura es irreversible, y como resultado genera una entropía. La generación de entropía siempre está acompañada por la destrucción de la exergía.
Transferencia de exergía por Trabajo, W
En el caso de un sistema que involucra trabajo de frontera, como un dispositivo cilindro-émbolo, el trabajo realizado para empujar el aire atmosférico durante la expansión no puede transferirse, entonces debe retirarse.
Transferencia de exergía por Masa, m
· Observe que la transferencia de calor por calor Xcalor, es cero para los sistemas adiabáticos
7.5. El principio de disminución de energía.
El principio de energía mínima es esencialmente segunda ley de la termodinámica. Declara que, para un sistema cerrado, con parámetros externos constantes y entropía, la energía interna disminuirá y su valor será cercano al mínimo en el equilibrio.7.6. Balance de energía.
Es un conjunto de relaciones de equilibrio que cuantifica los fluidos del proceso de producción, intercambio, transformación y consumo final de energía, expresados en una unidad común Peta Joules (PJ), en un periodo anual dentro de un territorio estatal, municipal o regional.
7.7. Relaciones de Maxwell.
Las relaciones de Maxwell son un conjunto de ecuaciones termodinámicas que se derivan del teorema de Clairaut (también conocido como teorema de Schwarz o teorema de la igualdad de las derivadas cruzadas o segundas derivadas) y de las definiciones de los potenciales termodinámicos (ecuación constitutiva asociada a un sistema termodinámico que tiene dimensiones de energía potencial). Estas relaciones se denominan así por el físico del siglo XIX James Clerk Maxwell.
La estructura de las relaciones de Maxwell es una declaración de igualdad entre las segundas derivadas para funciones continuas. A partir del hecho que el orden de diferenciación de una función analítica de dos variables es irrelevante (teorema de Schwarz). En el caso de relaciones de Maxwell, la función a considerar es un potencial termodinámico xi y xj es dos variables naturales diferentes para ese potencial:
7.8. La ecuación de Clapeyron.
7.9. Relaciones generales para dU, dH, dS, Cv y Cp
Al sustituir esto en la ecuación se obtiene la relación deseada para du:
7.10. El coeficiente Joule – Thomson.
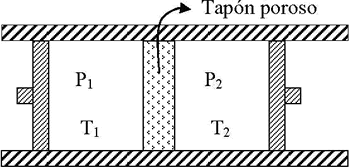
El coeficiente de Joule-Thomson se define como la variación de T con P a H constante (ecuación 5). Para poder determinar el valor de μJT, sería entonces necesario diseñar un experimento en el que se midiera la temperatura del sistema mientras que su presión varía a H constante.
El modelo matemático de la Primera Ley de la Termodinámica acoplado a un volumen de control (dispositivo de estrangulamiento) con una entrada y una salida, se llega a la conclusión de que la entalpia a la entrada es la misma que a la salida.
7.11. Cambios de energía interna, entalpía y entropía de gases reales.













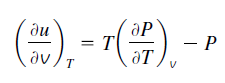








Comentarios
Publicar un comentario